机器学习必过的坎-梯度
CS231n课程笔记翻译:反向传播笔记 - 知乎
梯度 偏导数 方向导数
多元函数的 切向量和法向量 切平面方程 法线方程
(F'x,F'y,F'z)是曲线的法向量,
(dx,dy,dz)则是曲线的切向量 (x-x_, y-y_0, z-z_0)
法平面 : 与过空间一点M_0的切线互相垂直的平面叫法平面
小谈导数、梯度和极值 - JerryLead - 博客园
方向导数与梯度 -切线和法平面方程
ML涉及的数学 - Roach's Blog
为什么梯度反方向是函数值局部下降最快的方向?
为什么梯度的负方向是局部下降最快的方向?
Understand gradient descent
机器学习概念:梯度下降 - iKanG
梯度、方向導數與切平面.pdf
深度学习基础(1) 导数、偏导数、方向导数、梯度 - 作业部落 Cmd Markdown 编辑阅读器
如何直观理解方向导数,以及梯度
切向量和梯度的关系 - CSDN博客
三维空间曲面的切平面以及在某一点上的切线,法线 - CSDN博客
导数的理解
一苹果为例: 金额=数量x价格
dy = f’(x) dx 可得
f‘(x) 是支付金额关于苹果价格的导数 假设等于 2.2
那个价格每上涨 1元 总的支付金额就要上涨 2.2 元,如果价格上涨很小的值,那个总金额就会上涨那个很小值的2.2倍,
导数的好处,在于不用进行链式递归,直接通过源头和最终结果之间的关系
比如 金额关于苹果数量的导数 金额关于苹果消费税的导数
关于梯度与法向量的理解:
梯度定义为指向函数增长最快的方向(对隐函数来说其实存在降维了),其大小反映了函数增长的快慢。
梯度方向与 [垂直于等高面的法向量] 的方向相同。
设隐函数 f(x,y)=x2+y2,在空间中是一个锥面,其梯度为(2x,2y),一直不能理解这为什么是法向量的方向?垂直于锥面应该是在-z方向有一个量才对啊。(这里是最容易迷糊的) 错!!!
梯度里面包含的变量只有x和y,所以梯度变量只在x,y二维平面有意义(就是降维了),这里的梯度指向始终在(x,y)平面方向。如果把函数f(x,y)=x2+y2=C画出来,事实上是x,y二维平面上的一个圆。在某一点(x_0,y_0)上,其梯度(2x,2y)总是垂直指向外面更大的圆,此即指向增长最快的方向。
再引用维基上的两个例子:
定义在二维平面在(x,y)点上山的高度为h,则梯度指向高度变换最快的方向,仍然是在(x,y)平面上。
室内每个点的温度定义为一个数量场,则某点的梯度指向温度变化最大的方向。
一直疑惑,在一元方程中,比如y=x上,梯度的法向量作何解释?
y=x这个是二元方程 ,等价线为0 用隐函数表示为$F(x,y)= x-y$,当F(x,y)=0的梯度分析
事实上,此时的梯度就是导数。(1,-1)
导数和微分的本质(对一元函数)
导数,是一个极限值,是变化率,是描述函数在一点处的变化快慢的趋势 $f'(x)=\frac {df(x_0)}{dx}$
全导数非常简单,其实全导数本质上就是一元函数的导数。他是针对复合函数而言的定义。比如z=f(x,y),x=u(t),y=v(t)。那么z关于t的导数就是全导数。所以我说本质上就是个一元函数的导数,z本质上就是个关于t的一元函数。因此全导数没什么难于理解的,只不过为了复数函数的求导而被定义了出来。对于真正的多元函数是没有全导数这一说的,只有偏导数、偏微分和全微分
微分,是一个线性函数,就是切线,其意义就是变化的具体数值,描述函数在一点处发生一个无穷小区间的变化量的线性逼近 $dy=f'(x)dx$
是一个极限值;是当自变量x变化了一点点(dx)而导致了函数(f(x))变化了多少。
比如,国民收入Y=f(x),x是消费,那x变化了dx时,会导致Y变化多少呢?变化dY,这就是微分,而dY/dx就是这个单变量函数的导数。把微分dY视为dx的线性函数,那么导数就是这个线性函数的系数:注意,这个视角甚至可以推广到微分流形、泛函,等你以后深入学习到更高的层次就会知道,在这里打个伏笔。
差分,是一个有限值;粗糙地讲,就是离散化的微分,即$\Delta y$。差分Δy的无穷小就是微分 dy 。
Δx 对应切线的增量就是 dy 即 f'(x)dx
Δx 对应函数的增量就是 Δy 若是凸函数 则 Δy>dy
导数:是指函数在某一点处变化的快慢,是一种变化率。
微分:是指函数在某一点处(趋近于无穷小)的变化量,是一种变化的量。
全微分: 而对于多元函数而言,全微分就是指在各个自变量处的微分的和。也就是说总的变化量指各个分变化量的和,这样子就比较容易理解了。比如三元函数,所以$dz=z_xdx+z_ydy$。
导数和微分的关系类似于速度和路程。也就是说两个变化量之间的比值为,衡量变化快慢的变化率,比如速度就是路程的变化量和时间的变化量的比值。
无穷小: ex:同样一根稻草,如果是放在骆驼身上的一根稻草就是无穷小,但是压死骆驼的最后一根稻草就不是无穷小了
方向导数:是一个数;反映的是f(x,y)在P0点沿方向v的变化率。
方向导数:给一个方向,出一个实数(函数/标量场沿该方向的变化率)。
偏导数:是多个数(每元有一个);是指多元函数沿坐标轴方向的方向导数,因此二元函数就有两个偏导数。
偏导函数:偏导数是偏导函数在指定点的函数值,因此在求偏导数时,也可先求出偏导函数,然后再将点代入偏导函数,从而求出函数在此点的偏导数。
梯度:是一个向量;每个元素为函数对一元变量的偏导数;它既有大小(其大小为最大方向导数),也有方向。
梯度:给一个函数/标量场,出一个矢量场(方向为每点方向导数值最大的方向,大小为其变化率的矢量组成的矢量场)
切平面: 过A点有无数条切线,这些切线肯定在同一个平面(?),这个过A点的平面就是切平面
概念 物理意义
导数 标量 函数在该点的瞬时变化率
偏导数 标量 函数在坐标轴方向上的变化率
方向导数 标量 函数在某点沿某个特定方向的变化率
梯度 矢量 函数在该点沿所有方向变化率最大的那个方向
导数
导数的定义:
\[f'(x_0) = \lim\_{\Delta x \to 0}\frac{\Delta y}{\Delta x} = \lim\_{\Delta x \to 0}\frac{f(x_0+\Delta x) - f(x_0)}{\Delta x} = \frac {df(x_0)}{dx} =\frac {d}{dx}f(x_0) \]
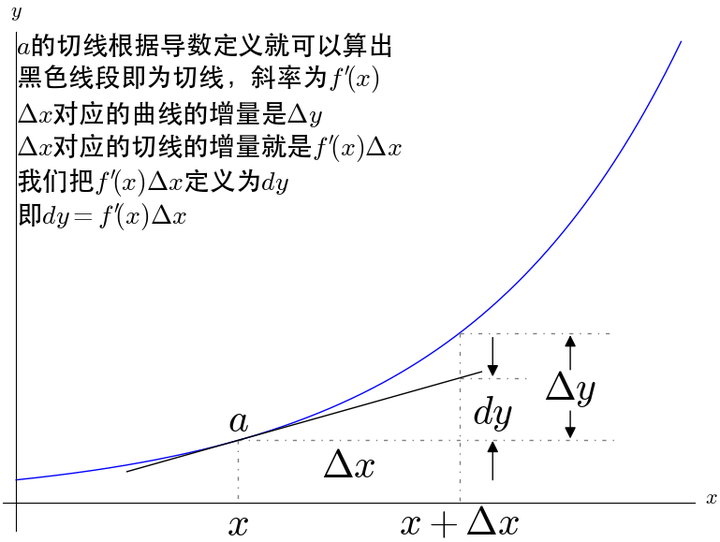
当函数 $y=f(x)$ 的自变量 $x$ 在一点 $x_0$ 上产生一个增量Δx时,函数输出值的增量 Δy 与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作$f'(x_0)$或$\frac {df(x_0)}{dx}$。
除了切线的斜率,导数还表示函数在该点的变化率
偏导(Partial Derivative)
既然谈到偏导数,那就至少涉及到两个自变量,一元函数导数只有两个方向,沿x轴的正方向和负方向,是没有偏导数.
这就是''f''关于''y''的偏导数,在这裡,∂是一个弯曲的''d'',称为'''[[偏导数符号]]'''。为了把它与字母''d''区分,∂有时读作“der”、“del”、“dah”或“偏”,而不是“dee”。
偏导数定义为:
\[\frac{\partial f}{\partial x_i}(x_0,x_1,\ldots,x\_{n}) = \lim\_{\Delta x \to 0}\frac{\Delta y}{\Delta x}= \lim\_{\Delta x \to 0}\frac{f(x_0,x_1,\ldots,x_i+\Delta x,\ldots,x_n) - f(x_0,x_1,\ldots,x_n)}{\Delta x}\]
可以看到,导数与偏导数本质是一致的,都是当一个自变量的变化量趋于0时,函数值的变化量与自变量变化量比值的极限
偏导只是二元函数沿着坐标轴 x 或者 y 的变化率, 但是能否求沿着任意方向的变化率呢? 当然可以了, 这就是方向导数(Directional Derivative). 而其中方向导数取最大值的方向就是梯度(Grad )啦, 也就是函数变化率最大的方向,
梯度
梯度公式:
grad f
梯度方向与曲线的切向量垂直,即梯度方向是法向量方向
Nabla算子 其形式化定义为:$\nabla = {d \over dr}$
在n维空间中,分母dr为含n个分量的向量,因而$\nabla$本身就是个n维向量[[算子]]。
三维情况下,$\nabla = {\frac{\partial }{\partial x}}\mathbf{i}+ {\frac{\partial }{\partial y}}\mathbf{j}+ {\frac{\partial }{\partial z}}\mathbf{k}$ 或 $\nabla = ({\frac{\partial }{\partial x}},{\frac{\partial }{\partial y}}, {\frac{\partial }{\partial z}})$
函数z=f(x,y)在点P0处的梯度方向是函数变化率(即方向导数)最大的方向
本来梯度就不是横空出世的,当我们有了这个需求(要求一个方向,此方向函数值变化最大),得到了一个方向,然后这个方向有了意义,我们给了它一个名称,叫做梯度
梯度:是一个矢量,其方向上的方向导数最大,其大小正好是此最大方向导数
梯度是方向导数取得最大值的方向
有一种通俗的的理解,梯度是导数的高维形式,导数是增长的方向,所以梯度其实是增长的方向,那么,梯度的反方向就是增长的反方向,下降。
方向导数就是梯度点乘单位向量啊,某一点的梯度是固定向量,所以点乘梯度方向的单位向量的方向导数最大,负方向的最小
方向导数(Directional Derivative).
方向导数: 反映的是 $f(x,y)$ 在P0点沿方向u的变化率。
方向导数定义为:
\[\frac{\partial}{\partial l} f(x_0,\dots,x_n) = \lim\_{t \to 0} \frac{\Delta y}{\Delta x} = \lim\_{t \to 0} \frac{f(x_0+\Delta x_0,\dots,x_i+\Delta x_i,\dots,x_n+\Delta x_n) - f(x_0,\ldots,x_i,\dots,x_n)}{t}\]
\[t = \sqrt{(\Delta x_0)^2+\cdots+(\Delta x_j)^2+\cdots+(\Delta x_n)^2}\]
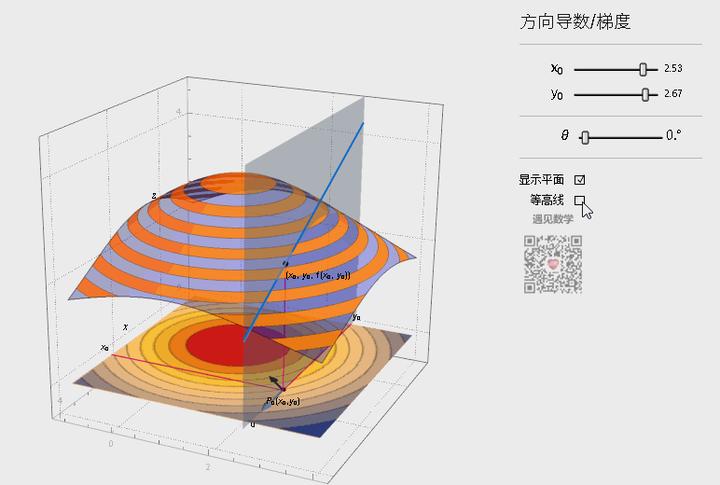
黑色箭头是梯度(每个点都有自己的梯度),蓝色箭头应该是求导方向,方向导数应该是一个数,当这两个方向重合时,方向导数最大。
原来我们学到的偏导数指的是多元函数沿坐标轴的变化率,但是我们往往很多时候要考虑多元函数沿任意方向的变化率,那么就引出了方向导数.
那么我们来考虑如何求出u 方向的斜率,可以类比于前面导数定义,得出如下:
方向导数公式:
设f(x,y)为一个二元函数,$u =cos\theta i+sin\theta j$ 为一个单位向量,如果下列的极限值存在
\[\lim\_{t \to 0}{\frac{f(x_0+tcos\theta ,y_0+tsin\theta )-f(x_0,y_0)}{t}}\]
此方向导数记为 $D_{u}f$
则称这个极限值是f沿着u方向的方向导数,那么随着$\theta$ 的不同,我们可以求出任意方向的方向导数.这也表明了方向导数的用处,是为了给我们考虑函数对任意方向的变化率.
$u=cos\theta i+sin\theta j$
任意方向的单位向量 $u=cos\theta i+sin\theta j$
其中 $i$ 是x方向的单位向量, $j$ 是y方向的单位向量, $θ$ 是此向量与 x 轴正向夾角。依据$θ$ 的不同,单位向量u可以表示对任何方向导数的方向
有时单位向量也记做 $u=cos\theta i+cos\beta j$ ($\alpha + \beta =90^\circ$ )
- 偏微分形式
在求方向导数的时候,除了用上面的定义法求之外,我们还可以用偏微分来简化我们的计算.
表达式是:$D_{u}f(x,y)=f_x(x,y)cos\theta +f_y(x,y)sin\theta$ (至于为什么成立,很多资料有,不是这里讨论的重点)
那么一个平面上无数个方向,函数沿哪个方向变化率最大呢?
目前我不管梯度的事,我先把表达式写出来:
\[D_uf(x,y)=f_x(x,y)cos\theta +f_y(x,y)sin\theta\]
设
\[A=(f_x(x,y),f_y(x,y)),I=(cos\theta,sin\theta)\]
那么我们可以得到:
\(D\_{u}f(x,y)=A\bullet I=\left| A \right| *\left| I \right| cos\alpha\) ($\alpha$ 为向量$A$与向量$I$之间的夹角)
那么此时如果 $D_{u}f(x,y)$ 要取得最大值,也就是当 $\alpha$ 为0度的时候,也就是向量I(这个方向是一直在变,在寻找一个函数变化最快的方向)与向量A(这个方向当点固定下来的时候,它就是固定的)平行的时候,方向导数最大.方向导数最大,也就是单位步伐,函数值朝这个反向变化最快.
好了,现在我们已经找到函数值下降最快的方向了,这个方向就是和A向量相同的方向.那么此时我把A向量命名为梯度(当一个点确定后,梯度方向是确定的),也就是说明了为什么梯度方向是函数变化率最大的方向了!!!(因为本来就是把这个函数变化最大的方向命名为梯度)
法线向量
如何理解三维曲面的法线向量公式?
三维空间中的曲面$F(x,y,z)=c$ 可理解为三维空间中的标量场$F(x,y,z)$的等值面,$\nabla F=(F_x,F_y,F_z)$
是每一点处的梯度,也就是值的变化最大的方向,直观上就是该等值面的法向方向。
- 梯度的定义是:对任意$\boldsymbol{v} \in \mathbb{R}^3$,$(\nabla f)\cdot\boldsymbol{v}=\nabla_{\boldsymbol{v}}f$
,其中$\nabla_{\boldsymbol{v}}f$ 指 $f$ 在$\boldsymbol{v}$ 方向上的方向导数。点乘和方向导数都是有明确定义的 ($\boldsymbol{v}$ 方向上的方向导数可理解为$f(\boldsymbol{x}+\alpha\boldsymbol{v})$ 对$\alpha$
求导),且不依赖于具体的坐标系,因而梯度是不依赖于具体坐标系的。 - 对于曲面$F(x,y,z)=c$
,一点处的切平面上的任一矢量$\boldsymbol{v}$
,满足$\nabla_{\boldsymbol{v}}F=0$
,因而$(\nabla F)\cdot\boldsymbol{v}=0$
,即梯度与切平面垂直。
所以,梯度的定义实际上就规定了它的唯一方向:与切平面垂直。那么原答案错的何处呢?
- 考虑曲面时,全微分没意义。处理曲面的工具是微分几何,依据是切平面上的局部坐标系,而全微分显然用了全局坐标系。
- 如果一定要用全局坐标系,并把dx,dy,dz理解坐标微元,它们显然与切平面不对齐。强制要求它们与切平面对齐,就得到一个处处变化的局部坐标系,实际上又回到了微分几何那一套。
那为什么一般都用$\nabla=(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})$
这个偏微分定义呢?它用的好像是全局坐标呀?
- 如果不考虑曲面性质,用全局坐标并无不妥。因为梯度与坐标系无关,这个定义只是它在一个具体坐标系下的表现形式。
- 为什么是这个形式呢?我们从梯度的原始定义出发,欲求梯度,需要先求切平面方程。对于曲面$F(x,y,z)=c$
,它在某点$(x,y,z)$
处的切平面方程的形式为$Ax+By+Cz=d$
,这实际上是$F(x,y,z)$
的一阶近似,因而系数就是那三个偏微分,这也就是梯度的偏微分定义的来源。
梯度下降
假设我们有一个函数 y = f (x),其中 x 和 y 是实数。这个函数的 导数(derivative)
记为 f′(x) 或dy/dx f′(x) 代表 f (x) 在点 x 处的斜率。换句话说,它表明如何缩
放输入的小变化才能在输出获得相应的变化:f (x + ε) ≈ f (x) + εf′(x)。
因此导数对于最小化一个函数很有用,因为它告诉我们如何更改 x 来略微地改
善 y。例如,我们知道对于足够小的 ε 来说,f (x − εsign(f′(x))) 是比 f(x) 小的。因
此我们可以将 x 往导数的反方向移动一小步来减小 f (x)。这种技术被称为 梯度下降
(gradient descent)(Cauchy, 1847)。图 4.1 展示了一个例子。
当 f′(x) = 0,导数无法提供往哪个方向移动的信息。f′(x) = 0 的点称为 临界
点(critical point)或 驻点(stationary point)。一个 局部极小点(local minimum)
意味着这个点的 f (x) 小于所有邻近点,因此不可能通过移动无穷小的步长来减小
f (x)。一个 局部极大点(local maximum)意味着这个点的 f (x) 大于所有邻近点,因
此不可能通过移动无穷小的步长来增大 f (x)。有些临界点既不是最小点也不是最大
1
译者注:与通常的条件数定义有所不同。4.3 基于梯度的优化方法
图 4.1: 梯度下降。梯度下降算法如何使用函数导数的示意图,即沿着函数的下坡方向(导数反方
向)直到最小。
点。这些点被称为 鞍点(saddle point)