贝叶斯定理

Think Bayes - 我所理解的贝叶斯定理
MLE MAP
- 频率学派 - Frequentist - Maximum Likelihood Estimation (MLE,最大似然估计)
- 贝叶斯学派 - Bayesian - Maximum A Posteriori (MAP,最大后验估计)
频率学派和贝叶斯学派对世界的认知有本质不同:频率学派认为世界是确定的,有一个本体,这个本体的真值是不变的,我们的目标就是要找到这个真值或真值所在的范围;而贝叶斯学派认为世界是不确定的,人们对世界先有一个预判,而后通过观测数据对这个预判做调整,我们的目标是要找到最优的描述这个世界的概率分布
贝叶斯定理是统计学中非常重要的一个定理,以贝叶斯定理为基础的统计学派在统计学世界里占据着重要的地位,和概率学派从事件的随机性出发不同,贝叶斯统计学更多地是从观察者的角度出发,事件的随机性不过是观察者掌握信息不完备所造成的,观察者所掌握的信息多寡将影响观察者对于事件的认知。
贝叶斯学派: θ是一个随机变量,符合一定的概率分布。在贝叶斯学派里有两大输入和一大输出,输入是先验 (prior)和似然 (likelihood),输出是后验 (posterior)。
先验,即P(θ),指的是在没有观测到任何数据时对θ的预先判断,例如给我一个硬币,一种可行的先验是认为这个硬币有很大的概率是均匀的,有较小的概率是是不均匀的;似然,即P(X|θ),是假设θ已知后我们观察到的数据应该是什么样子的;后验,即P(θ|X),是最终的参数分布。
贝叶斯估计的基础是贝叶斯公式,如下: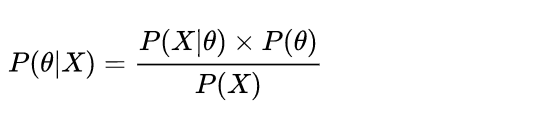
同样是抛硬币的例子,对一枚均匀硬币抛5次得到5次正面,如果先验认为大概率下这个硬币是均匀的 (例如最大值取在0.5处的Beta分布),那么P(head),即P(θ|X),是一个distribution,最大值会介于0.5~1之间,而不是武断的θ= 1。
条件概率和全概率
在介绍贝叶斯定理之前,先简单地介绍一下条件概率,
条件概率
描述的是事件 A 在另一个事件 B 已经发生条件下的概率,记作$P(A|B)$ A 和 B 可能是相互独立的两个事件,也可能不是:
- $P(A|B)=\frac{P(A \cap B)}{P(B)}$
同时发生概率
$P(A \cap B)$ 表示A,B 事件同时发生的概率,
如果 A 和 B 是相互独立的两个事件,那么:
- $P(A|B)= \frac{P(A\cap B)}{P(B)} = \frac{P(A) \times P(B)}{P(B)}=P(A)$
上面的推导过程反过来证明了如果 A 和 B 是相互独立的事件,那么事件 A
发生的概率与 B 无关。
稍微做一下改变:
- $P(A\cap B)=P(A|B) \times P(B)$
考虑到先验条件 B 的多种可能性,这里引入
全概率公式:
$P(A) =P(A\cap B)+P(A\cap B^\complement) = P(A|B)\times P(B)+P(A|B^\complement) \times P(B^\complement)$
互补事件
这里 $B^\complement$ 表示事件 B 的互补事件,从集合的角度来说是 B 的补集:
$P(B)+P(B^\complement)=1$
条件概率和全概率公式可以通过韦恩图形象地表示出来: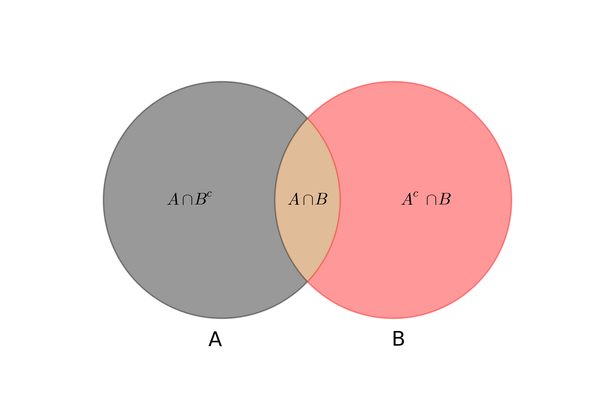
贝叶斯公式 依赖于条件概率和全概率
P(已知考试B发生了[考试及格],求是A发生的概率[A等生])= P(A发生的条件下B发生的概率[A等生及格]) x P(A发生的概率[A等生占比]) / P(B 发生的概率[及格的概率])
P(考试及格是优等生的[是条件概率]) = P(优等生的概率)xP(优等生及格的概率[也是条件概率]) / P(考试及格的概率[是全概率])
在条件概率和全概率的基础上,很容易推导出贝叶斯公式:
\[P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{P(B|A)\times P(A)}{P(B)}=\frac{P(B|A)\times P(A)}{P(B|A)\times P(A)+P(B|A^c)\times P(A^c)}\]
看上去贝叶斯公式只是把 A 的后验概率转换成了 B 的后验概率 + A
的边缘概率的组合表达形式,因为很多现实问题中
很难直接观测,但是
却很容易测得,利用贝叶斯公式可以方便我们计算很多实际的概率问题。
一个很有意思的例子
在生活中,几乎所有人(包括统计学者)都会无意识地将两个事件的后验概率混淆,即:
最经典的一个例子就是疾病检测,假设某种疾病在所有人群中的感染率是0.1%,医院现有的技术对于该疾病检测准确率为
99%(已知患病情况下, 99% 的可能性可以检查出阳性;正常人 99%
的可能性检查为正常),如果从人群中随机抽一个人去检测,医院给出的检测结果为阳性,那么这个人实际得病的概率是多少?
很多人会脱口而出
\"99%\",但真实概率远低于此,因为他们把两个后验概率搞混了,如果用 A
表示这个人患有该疾病,用 B 表示医院检测的结果是阳性,那么
表示的是「已知一个人得病的情况下医院检测出阳性的概率」,而我们现在问的是「对于随机抽取的这个人,已知检测结果为阳性的情况下这个人患病的概率」,即
我们可以用贝叶斯定理来计算这个人实际得病的概率:
其中:
将上面的概率代入到贝叶斯公式中,可得:
这个公式在这里的实际意义是什么?让我们用图来解释(图中概率经过四舍五入,考虑到图片的尺寸,面积并没有和概率严格对应起来):

从贝叶斯的角度来看,随意选取的一个被测者,由于信息并不充分,未检测之前有假阳性、真阳性、假阴性和真阴性四种可能,这些可能性由检测技术和该疾病的感染率决定,当检测结果为阳性的时候,只剩下真阳性和假阳性两种可能,而真阳性的概率仅为假阳性的十分之一,贝叶斯公式在这里的实际意义是:
即使被医院检测为阳性,实际患病的概率其实还不到10%,有很大可能是假阳性,往往需要复检来确定是否真的患病,让我们再来计算初检和复检结果都为阳性时,患病的可能性。假设两次检查的准确率相同,都是99%,这里令
B 为第一次检测结果为阳性,C 为第二次检测结果为阳性,A
为被检测者患病,那么两次检测结果都是阳性患病的概率可以表示为:
\
其中:
代入后可得:
可见复检结果大大提高了检测的可信度,联系上面的图,复检的意义在于大幅减少假阳性的可能(0.01-> 0.0001)从而提高阳性检测的准确性。