牛顿迭代法求近似值Newton's method
如何不依靠计算器和数学用表，手动给非平方数开根号？ - 知乎
牛顿迭代法求解平方根 - YoungGy的专栏 - CSDN博客
牛顿迭代法(Newton's Method) - 無名黑洞 - CSDN博客
牛顿迭代法 · 用Python学微积分
牛顿迭代法
第一步就是转换（关键思想）：
问题：试求 √2 的近似值。转化为求解函数 f(x)=x^2−2 的根，就是球f(x)=
原命题等价于求函数𝑓(𝑥)=𝑥^2−2的零点。
第二步 是迭代
- 使用牛顿迭代公式求解方程
求解步骤： - 原函数：f(x)=x^m−a
- 原函数的导函数：f′(x)=mxm−1f′(x)=mxm−1
- 使用牛顿迭代公式xn+1=xn−f(xn)f′(xn)xn+1=xn−f(xn)f′(xn)：
xn+1=xn−f(xn)f′(xn)=xn−xmn−amxm−1n
xn+1=xn−f(xn)f′(xn)=xn−xnm−amxnm−1 - 示例
3.1 利用牛顿迭代公式求解平方根
求解平方根也就是求解函数f(x)=x2−a，f(x)=0f(x)=x2−a，f(x)=0 的根。根据上述的求解过程f′(x)=2xf′(x)=2x ， 带入牛顿迭代公式：
xn+1=xn−x2n−a2xn
————————————————
版权声明：本文为CSDN博主「Robin__Chou」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/Robin__Chou/article/details/52103009
牛顿-拉弗森方法的代数解法
比如求平方根：$x2=78$，可以转为求$x2-78=0$
已知曲线方程f(x)，我们在$xn$点做切线，求$x{n+1}$：
容易得出，$x_n$点的切线方程为：$f(x_n)+f'(x_n)(x-xn)$。
要求$x{n+1}$，即相当于求$f(x_n)+f'(x_n)(x-x_n)=0$的解，即
\(f(x_n)+f'(x_n)(x_{n+1}-x_n)=0\implies：\)
$x_{n+1}=x_{n}-{\frac {f(x_{n})} {f'(x_{n})}}$。
一般用这种看起来很像长除法的技巧。举例来说，现在我要给15241.5788这个数，手算开方。那么，第一步：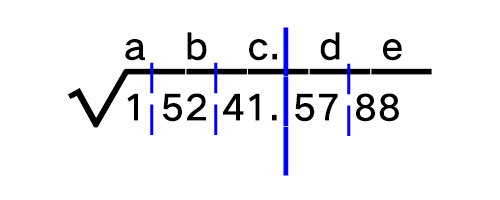
以小数点为界，从中间向两边，每两位画一条分割线。每个区块将对应方根的一位数（http://abc.de）。第二步：取最左区块，令a为满足“a的平方≤区块值”的最大值。比如区块值是5，那么a就是2（2*2=4≤5）；区块值是16，那么a就是4（4*4=16≤16）。这里区块值是1，那么a就是1，而且没有余数，直接把下一个区块（52）落下来，准备求b了。
第三步：敲黑板，划重点！手算开方里有一个很关键的套路公式：M=x*(20W+x)≤N。其中x是待求的方根一位数，W是已经解出的部分方根数值，N是落下来的数，20是个常数。其实第二步就是这个公式在W=0的情况下直接算x平方的特例罢了。现在对应着看，W是最上面那个1，N是52，x就是我们要算的未知数b：b(201+b)≤52。同上，还是要满足条件的b的最大值。易得b=2（2(201+2)=44≤52，取3就大了）。这步出现余数了：让52减去这个M（44），和下一个区块落到一起。
第四步：重复以上步骤即可。注意除了常数每个都是变量，W=12，N=841，即c(2012+c)≤841。解得c=3，M=729。W=123，N=11257，即d(20123+d)≤11257。解得d=4，M=9856。W=1234，N=140188，即e(201234+e)≤140188。解得e=5。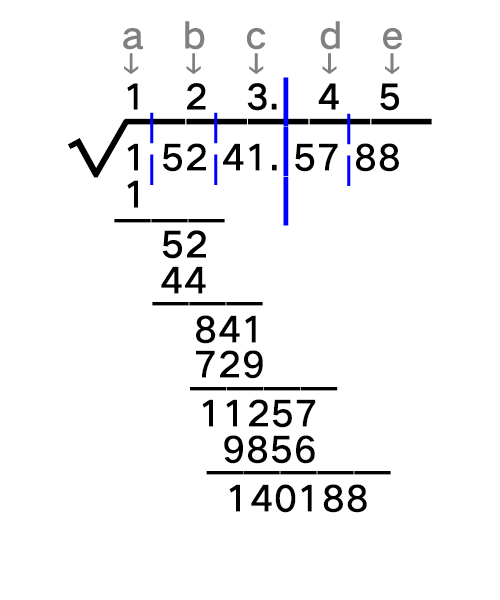
综上，我们得到一个数123.45，这就是咱手动所得的方根。计算器验证得，15241.5788开方=123.4567892017...受被开方数位数所限，如果需要更高精度，就得补零继续。想学开三次方根嘛？只要改动两处就好了：一，每三位数画一条分割线；二，套路公式改成：
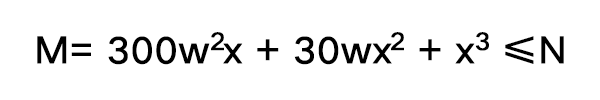（看来上面那个常数20是和要开几次方根有关的数，应该是来自 (10a+b)^2 = 100a+(20a+b)b 这个关系式，感谢评论区！）我以23.3的三次方12649.337验证一下给大家看看：W=0，N=12，即 a^3 ≤12。解得a=2，M=8。W=2，N=4649，解得a=3，M=4167。W=23，N=482337，解得a=3，M=482337。
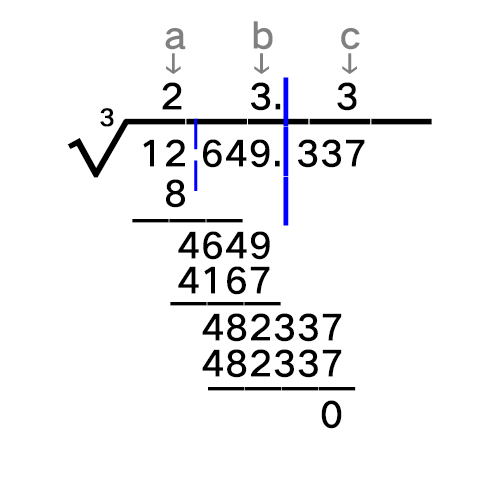完(zhen1)美(lei4)！