Gradient Descent
机器学习概念:梯度下降
学习梯度,需要一定的数学知识:导数(Derivative)、偏导数(Partial derivative)和方向导数(Directional derivative)。
1. 导数
一张图看懂,导数与微分:
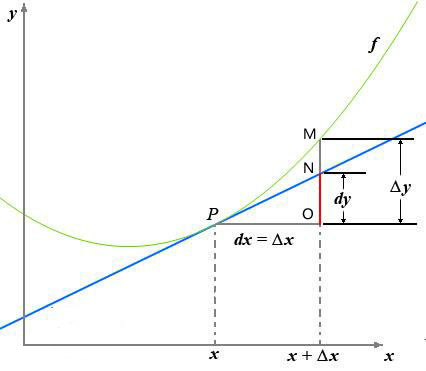
导数的定义如下:
$f'(x_0)=\underset{\Delta x\rightarrow0}{lim}\frac{\Delta y}{\Delta x}=\underset{\Delta x \rightarrow 0}{lim}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$
反应的是函数$y=f(x)$在某一点处沿$x$轴正方向的变化率
函数$f(x)$在$x$轴上沿着$x$轴正方向的变化趋势,导数的绝对值越大,变化趋势越明显
- 如果导数值为正的话,说明$f(x)$在$x$点沿着$x$轴正方向是趋于增加的
- 如果导数值为负的话,说明$f(x)$在$x$点沿着$x$轴正方向是趋于减少的
对于上式子
| 符号 | 意义 |
|---|---|
| $\Delta x$ | $x$的变化量 |
| $dx$ | $x$的变化量$\Delta x$趋于0时,记作微元$dx$ |
| $\Delta y$ | $\Delta y=f(x_0+\Delta x)-f(x_0)$指函数的改变量 |
| $dy$ | $dy=f'(x_0)dx$是切线的改变量 |
当$\Delta x \rightarrow 0$时,$dy$与$\Delta y$都是无穷小,$dy$是$\Delta y$的主部,即:$\Delta y=dy+o(\Delta x)$ $o()$:低阶无穷小
2. 偏导数
偏导数的定义如下:
$\frac{\partial}{\partial x_j}f(x_0,x_1,\cdots,x_n)=\underset{\Delta x \rightarrow 0}{lim} \frac{\Delta z}{\Delta x}=\underset{\Delta x \rightarrow 0}{lim}\frac{f(x_0,x_1,\cdots,x_n)-f(x_0,x_1,\cdots,x_n)}{\Delta x}$
\[\frac{\partial f}{\partial x_i}(x_0,x_1,\ldots,x_n) =\lim_{\Delta x \to 0} \frac{\Delta z}{\Delta x}= \lim_{\Delta x \to 0}\frac{f(x_0,x_1,\ldots,x_i+\Delta x,\ldots,x_n) - f(x_0,x_1,\ldots,x_n)}{\Delta x}\]
可以看到,导数与偏导数的本质都是一样的,当自变量的变化量趋于0时,函数值的变化量与自变量变化量比值的极限。直观的说,偏导数也就是函数在某一点上沿坐标轴正方向的变化率。
导数与偏导数的区别
导数:指的是一元函数中,函数$y=f(x)$在某一点处沿$x$轴正方向的变化率
偏导数:指的是多元函数中,函数$y=f(x_1,x_2,\cdots,x_n)$在某一点处沿某一坐标轴$(x_1, x_2, \cdots, x_n)$正方向的变化率
3. 方向导数
方向导数的定义如下:
$\frac{\partial}{\partial l}f(x_0,x_1,\cdots,x_n)=\underset{\rho \rightarrow 0}{lim}\frac{\Delta z}{\Delta x}=\underset{\rho \rightarrow 0}{lim}\frac{f(x_0+\Delta x_0,\cdots,x_j +\Delta x_j,\cdots,x_n+\Delta x_n)-f(x_0,\cdots,x_j,\cdots,x_n)}{\rho}$
其中: $\rho = \sqrt{(\Delta x_0)^2+\cdots+(\Delta x_j)^2+\cdots+(\Delta x_n)^2}$
导数与偏导数均为沿坐标轴正方向讨论函数的变化率,而方向导数,顾名思义,讨论函数在任意方向的变化率。即:某一点在某一趋近方向上的导数值
通俗的解释是:
我们不仅要知道函数在坐标轴正方向上的变化率(即偏导数),而且还要设法求得函数在其它特定方向上的变化率,而方向导数就是函数在其它特定方向上的变化率。
4. 梯度
梯度的定义如下:
$grad f(x_0,x_1,\cdots,x_n)=(\frac{\partial f}{\partial x_0},\cdots,\frac{\partial f}{\partial x_j},\cdots,\frac{\partial f}{\partial x_n})$
梯度的存在,为了回答一个问题:
函数在变量空间的某一点处,沿着哪一个方向有着最大的变化率
梯度的文字定义如下:
函数在某一点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,它的模为方向导数的最大值。
注意:
- 梯度是一个向量,有方向有大小
- 梯度的方向是最大方向导数的方向
- 梯度的值的最大方向导数的值
梯度即函数在某一点最大的方向导数,函数沿梯度方向,函数的变化率最大。
5. 梯度下降法
既然在变量空间的某一点处,函数沿梯度方向具有最大的变化率,那么在优化目标函数的时候,自然是沿着负梯度方向去减小函数值,来达到我们的优化目标
如何沿着负梯度方向减小函数值呢?因为梯度是偏导数的集合,如下:
\[gradf(x_0,x_1,\cdots,x_n)=(\frac{\partial f}{\partial x_0},\cdots,\frac{\partial f}{\partial x_j},\cdots,\frac{\partial f}{\partial x_n})\]
由于梯度和偏导数均为向量,由向量的运算法则可知,我们在每个变量轴上减小对应的变量值即可,梯度下降算法可描述为:
Repeat {
$x_0:=x_0-\alpha\frac{\partial f}{\partial x_0}$
$\cdots$
$x_j:=x_j-\alpha\frac{\partial f}{\partial x_j}$
$\cdots$
$x_n:=x_n-\alpha\frac{\partial f}{\partial xn}$
$\cdots$
}
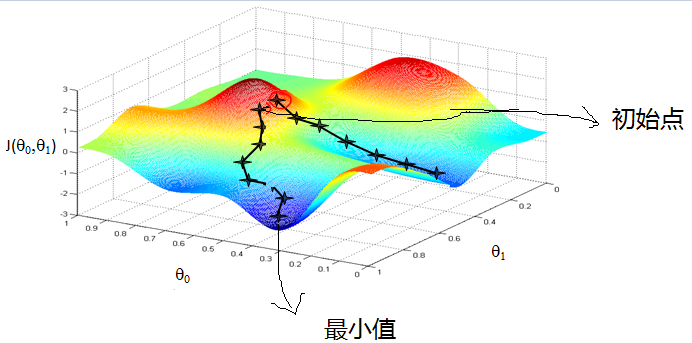
由这个可以很清楚的了解梯度下降的过程,类似人在高山上,如何快速下山
- 寻找下降速度最快的方向
- 向下走
- 循环步骤1和步骤2, 直到到达最小值(山底)
在这里,我们还需要了解几个概念:
5.1. 步长(learning rate)(学习速度)
步长决定了在梯度下降过程中,每一步沿梯度负方向前进的长度。
5.2. 特征(feature)
特征值的是样本输入部分,比如两个单特征样本\((x^{(0)}, y^{(0)}),(x^{(1)}, y^{(1)})\)则第一个样本的特征为\(x^{(0)}\),第一个样本的输出为\(y^{(0)}\)
5.3. 假设函数(hypothesis function)
在监督学习中,为了拟合输入样本,而使用假设函数,记作$h_\theta(x)$.比如对于单个特征的m个样本$(x^{(i)}, y^{(i)}) (i=1,2,\cdots,m)$可以采用拟合函数如下:$h_\theta(x)=\theta_0+\theta_1 x$
5.4. 损失函数(loss function)
为了评估模型拟合的好坏,通常损失函数来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。在线性回归中,损失函数通常为样本输出和假设函数的差取平方,比如对于m个样本$(x_i,y_i)(i=1,2,\cdots,m)$采用线性回归,损失函数为:
\[J(\theta_0,\theta_1)=\frac{1}{2}\sum^{m}_{i=1}(h_\theta(x_i)-y_i)^2\]
这里的$\frac{1}{2}$是为了方便求导
其中$x_i$表示第$i$个样本特征,$yi$表示第 $i$ 个样本对于的输出,$h\theta(x_i)$ 为假设函数。
梯度下降算法与线性回归算法比较

6. 梯度下降算法详细
梯度下降算法可以有代数法和矩阵法(也称向量法)
相比于代数法,矩阵法更加简洁,这里就不介绍代数法了,感兴趣的读者可以阅读:
梯度下降算法的矩阵法
这里需要一定的矩阵 求导 知识
首先我们需要确定优化模型的假设函数和损失函数,对于线性回归来说:
假设函数:
$h_\theta(x_1,x_2,x\cdots,x_n)=\theta_o+\theta_1x_1+\cdots+\theta_nx_n$
矩阵表达方式为:$h_\theta(\boldsymbol X)=\boldsymbol X\theta$
其中:$\boldsymbol X$是大小为$m$x$n$的矩阵。m代表样本个数, n代表样本的特征数
$h_\theta(\boldsymbol X)$为$m$x1的向量、$\theta$为$n$x1的向量
损失函数:
$J(\theta)=\frac{1}{2}(\boldsymbol X\theta-\boldsymbol Y)^T(\boldsymbol X\theta-Y)$
其中:$\frac{1}{2}$是为了方便求导,$\boldsymbol Y$是样本的输出向量,维度为$m$x1
算法过程:
- 确定当前位置的损失函数的梯度,对于$\theta$向量,其梯度表达式如下:
$\frac{\partial}{\partial\theta}J(\theta)$
- 用步长乘以损失函数的梯度,得到当前位置下降的距离
$\alpha \frac{\partial}{\partial\theta}J(\theta)$ 这里设置$\alpha$为步长
确定$\theta$向量里的每个值,梯度下降的距离都小于$\varepsilon$,如果梯度下降的距离小于$\varepsilon$则算法终止,当前$\theta$向量即为最终结果。否则进行下一步
更新$\theta$向量,更新表达式如下: 更新结束后,将表达式传回步骤1
$\theta=\theta-\alpha\frac{\partial}{\partial}J(\theta)$
其中,损失函数对于$\theta$向量的偏导数计算如下:
$\frac{\partial}{\partial\theta}J(\theta)=\boldsymbol X^T(\boldsymbol X\theta-\boldsymbol Y)$
步骤4中$\theta$向量的更新表达式如下:
$\theta=\theta-\alpha \boldsymbol X^T(\boldsymbol X\theta-\boldsymbol Y)$
7. 梯度下降法大家族(BGD,SGD,MBGD)
7.1. 批量梯度下降法(Batch Gradient Descent)
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新。
\[\theta_i = \theta_i - \alpha\sum\limits_{j=0}^{m}(h_\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{(j)}) - y_j)x_i^{(j)}\]
由于我们有m个样本,这里求梯度的时候就用了所有m个样本的梯度数据。
7.2. 随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的m个样本的数据,而是仅仅选取一个样本j来求梯度。对应的更新公式是:
\[\theta_i = \theta_i - \alpha (h_\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{(j)}) - y_j)x_i^{(j)}\]
7.3. 小批量梯度下降法(Mini-batch Gradient Descent)
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷,也就是对于m个样本,我们采用x个样子来迭代,$1<x<m$。一般可以取x=10,当然根据样本的数据,可以调整这个x的值。对应的更新公式是:
\[\theta_i = \theta_i - \alpha \sum\limits_{j=t}^{t+x-1}(h_\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{(j)}) - y_j)x_i^{(j)}\]
8. 梯度下降法和其他无约束优化算法的比较
在机器学习中的无约束优化算法,除了梯度下降以外,还有前面提到的最小二乘法,此外还有牛顿法和拟牛顿法。
梯度下降法和最小二乘法相比,梯度下降法需要选择步长,而最小二乘法不需要。梯度下降法是迭代求解,最小二乘法是计算解析解。如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。但是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。
梯度下降法和牛顿法/拟牛顿法相比,两者都是迭代求解,不过梯度下降法是梯度求解,而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言,使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。
参考: https://www.cnblogs.com/pinard/p/5970503.html
机器学习概念:梯度下降 - iKanG